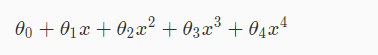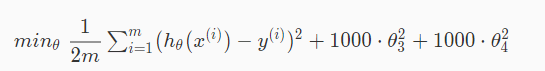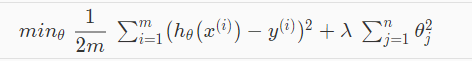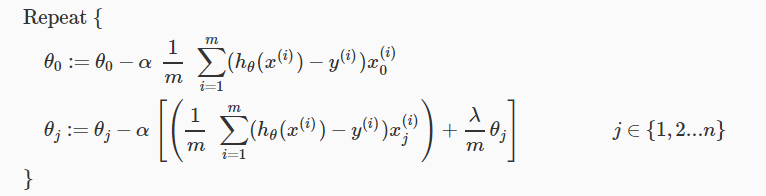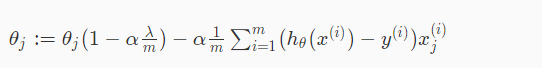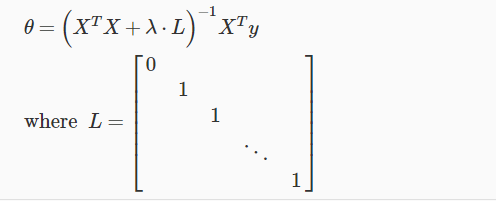In this post we will see how regularization works to remove the problem of overfitting .We will also check the cost function we will use when we were using regularization.
Cost Function
We can reduce the weight that some of the terms in our function carry by increasing their cost, if we have problem of overfitting from our hypothesis function.
For example suppose we wanted to make the below example function more quadratic:
We can do the work of making the function more quadratic by eliminating the influence of 4th and 5th term in above equation.Without directly deleting this terms we can modify the cost function as following:
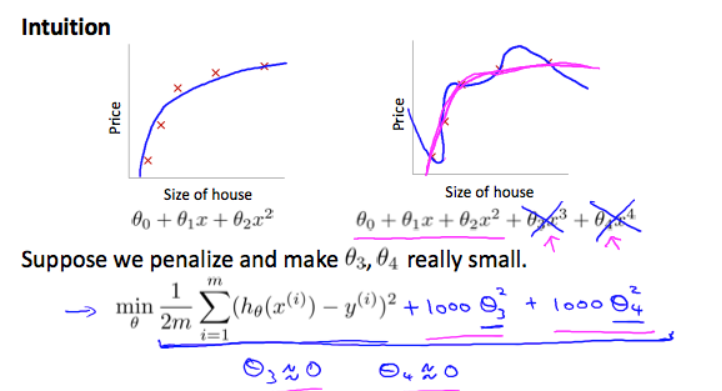
So we will get a intuition as following :
So finally we could regularize all of our theta parameters in a single summation as following:
In the above equation the parameter λ or lambda is called regularization parameter. By using this extra summation in cost function we can reduce overfitting as we can smooth the output of our hypothesis function. But if λ value is too large then it may also cause underfitting.
Regularized Linear Regression
In our earlier post’s we have seen two algorithms for linear regression:one is based in gradient descent and one is based on normal equation.So now we will take both of these algorithms and generalize them so that they will also work for in the case of regularized linear regression.
Gradient Descent
Because of the fact that we don’t want to penalize θ0, we will modify our gradient descent function to separate out θ0 from the rest of the parameters as following:
with some manipulation’s in the above equation we will get the following final equation:
In the above equation the first term 1 – αλ/m will always less than 1, because we have m larger and λ smaller and the second term is same as we used before.
Normal Equation
We will modify the normal equation as following to add regularization in it.
Regularized Logistic Regression
In our earlier post’s we have seen also two methods for linear regression:one is based in gradient descent and one is based on optimized algorithms.So now we will take both of these algorithms and generalize them so that they will also work for in the case of regularized logistic regression.
In the following image we will see that the pink line which is regularized function is removing the problem of overfitting which is there in non-regularized function shown by blue line:

So we will have following cost function in the logistic regression.
So we will add regularization to the above cost function by adding one term at the last as following:
The second term in the above equation is means to exclude that term as following:
So in this post we have discussed about how to add regularization in both linear regression and logistic regression.So we have added regularization in both gradient descent and normal equation method’s of linear regression and also added regularization in both gradient descent and advanced optimization techniques of logistic regression.