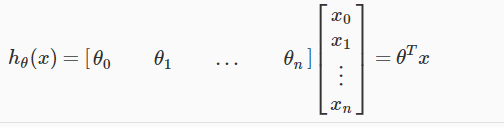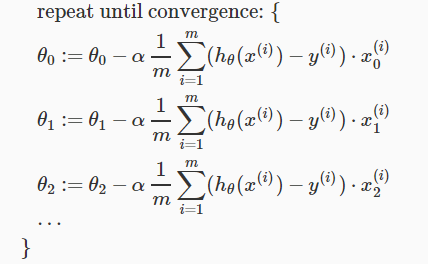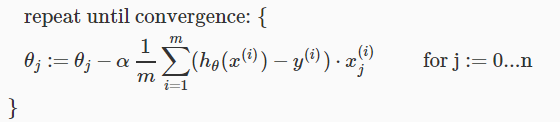In this post we will talk about Linear regression that will work with multiple variables or with multiple features.
In the earlier post we have discussed a linear regression that will work with only a single feature x,the size of the house and we wanted to use that to predict y the price of house.But now imagine that we have not only the size of the house as the feature or as a variable of which to try to predict the price,but we also know the number of bedrooms,number of floors and the age of the home in years.We will going to use x1,x2…..xn for the features we have,and y for the output variable price that we are trying to predict.
So we will use basically this notation in multi variable linear regression.
So our hypothesis function will also change as following:
Using the matrix multiplication properties we can represent that hypothesis function as following:
Now we will see how to use gradient descent for linear regression with multiple features.
We will have following gradient descent equation:
which is in general can be written as following:
Feature Scaling
If we have each of our input values in roughly same range then we can speed up our gradient descent.The reason behind this is because θ will descend slowly on large values and quickly on small ranges.
So ideally we can have this range to speed up our gradient descent.
−1 ≤ x(i) ≤ 1 or −0.5 ≤ x(i) ≤ 0.5
These are not exact requirements.So our main goal is to get all input variables roughly into above range.
We will use this two techniques to reach this goal: feature scaling and mean normalization
In feature scaling we will divide the input values by the range (i.e. the maximum value minus the minimum value) of the input variable.
In Mean normalization we will subtract the average value for an input variable from the values for that input variable resulting in a new average value for the input variable of just zero.
We can implement both of the above mentioned techniques by following formula.
xi:=(xi−μi)/si
here in the above formula μi is the average of all the values for feature (i) and si is the range of values (max – min), or si is the standard deviation.
Learning Rate
To debug a gradient descent: For that you can make a plot with number of iterations on the x-axis. Now after plotting no.of iterations, plot the cost function J(θ) over the number of iterations of gradient descent. If J(θ) will ever increases then we must have to decrease α.
We can also have Automatic convergence test in which we can declare a convergence if J(θ) ever decreases by less than E in any of one iteration, where E is some small value like 10^-3.
So if we have α too small then we will have slow convergence and if we have α too large then it may not converge.
So this is all about linear regression with multiple features, feature scaling and learning rate in that.