Time & Work – Dont Miss these amazing tricks

Time & Work based topic is one of the most beautiful questions that would appear in any aptitude or placement or government exams. If you love it, it will love you back for sure as it is one of the easiest understandable topics.

Here you will learn the best shortcut method to solve the time and work questions within seconds.

Table of content
1) Basics of time and work
2) Time and work questions – Left the work in between
3) Time and work – Alternate day work question
4) Time and work – People and work questions
5) Work and contribution questions
6) Some one left the work questions

Basic Time and Work Questions

Statement- A can do a piece of work in 20 days. What is it one day work ?
Solution –
A completes whole work in 20 days.
Assume total work = 1
A’s 1 day work = 1/20 [ This is also Efficiency of A ]

$Total days to complete work = \frac{1}{1 day work}$

Just remember the above thing and try to understand and every question will solve within seconds.

Note – In time and work questions work when work is not mentioned , assume work to be = 1 unit or simply 1.

Question ) A can do a piece of work in 20 days and B can do it in 15 days. How long will they take if both work together?
A) 62/7 days B) 60/7 days C) 66/7 days D) 67/7 days

Solution: We will solve this question by traditional method first.

Traditional Method
Assume total work = 1 [as explained above]
A can do complete work in 20 days.
A’s 1 day work = 1/20
B can do complete work in 10 days.
B’s 1 day work = 1/10
we have to find – how many days A and B will take to complete the work together.
A’s 1 day work + B’s 1 day work = $\frac{1}{20} + \frac{1}{15} = \frac{15+20}{300} = \frac{35}{300} = \frac{7}{60}$
Just apply the above logic
Total days to complete work is reciprocal of 1 day work
A and B can do total work in = $\frac{60}{7}$ days

Now LCM method – Padhle shortcut trick
Draw a table like Below and below table is self explanatory

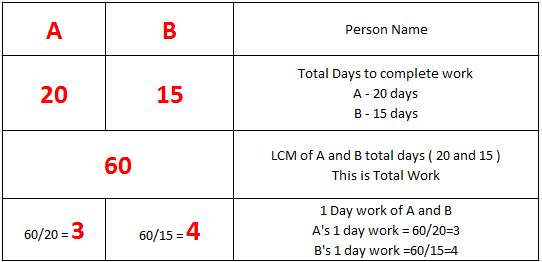
Now from the above table –
(A and B) 1 day work together = 3 + 4 = 7
Total work = 60 [ from above table]
Total days to complete work by A and B together = Total work / 1 day work
= 60 /7 days
Answer = (B) 60/7 Days

Practice LCM method again and again to become pro

Question) Jai can do a piece of work in 10 days and Veeru can do the same work in 20 days. With the help of Basanti, they finish the work in 5 days. How long will it take for Basanti alone to finish the work?
A) 20 days B) 10 days C) 35 days D) 15 days

Solution:
Use LCM method – Draw the table

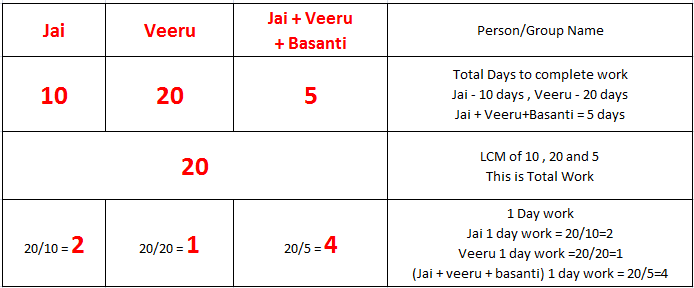
From above table
Jai 1 day work = 2
Veeru 1 day work = 1
Jai+Veeru+Basanti together 1 day work = 4
Basanti 1 day work = (Jai + veeru + basanti ) 1 day work – Jai 1 day work – Veeru 1 day work
= 4 – 2 – 1 = 1
Basanti 1 day work = 1
Total work = 20
Total days basanti need to complete work = 20 / 1 = 20 days
Answer: (A) 20 Days

Question) Frodo can do 1/2 of the work in 8 days while Bilbo can do 1/3 of the work in 6 days. How long will it take for both of them to finish the work?
A) 88/17 days B) 144/17 days C) 72/17 days D) 8 days

Solution –
Frodo can do 1/2 work in 8 days hence
Frodo can do total work in 8 * 2 = 16 days [ unitary method ]
Biblo can do 1/3 work in 6 days
Biblo can do total work in 6 * 3 = 18 days [ unitary method ]

Draw table now

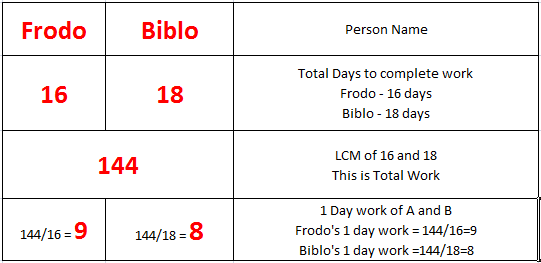
From above table
(Frodo and Biblo) 1 day work together = 9 + 8 = 17
Total work = 144 [ from above table]
Total days to complete work by Frodo and Biblo together = Total work / 1 day work
= 144 /17 days

Answer: (B) 144/17 Days.

Some one left the work – Time and work questions

Question ) A, B and C can complete a piece of work in 10, 12 and 15 days respectively. All three of them starts together but after 2 days A leaves the job and B left the job 3 days before the work was completed. C completed the remaining work alone. In how many days was the total work completed ?

Solution:

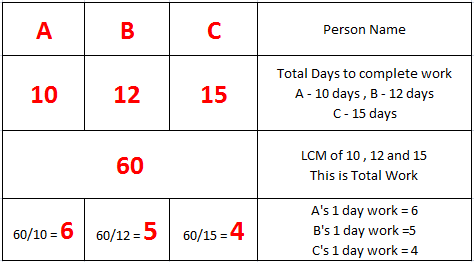
Now understand from the table –
let say Total work = 60 units
A’s 1 day work = 6 Units
B’s 1 day work = 5 Units
C’s 1 day work = 4 Units
( A + B + C ) 1 day work = 6 + 5 + 4 = 15 units
Understand question carefully now –
A left the work after 2 days and ( A + B + C ) start together , So ( A + B + C ) together did work for 2 days only ,
( A + B + C ) 1 day work = 15 units
( A + B + C ) 2 day work = 15 * 2 = 30 units
Total left work = 60 – 30 = 30 units

After 2 days only B and C are working together and B left 3 days before work was completed.
So last 3 days only C worked.
in Last 3 days , C completed work = 3 * ( C’s 1 day work ) = 3 * 4 = 12 units
Total work left now = 30 – 12 = 18 units

Now these 18 units completed by B and C together in between.
( B + C ) 1 day work = 5 + 4 = 9 units
( B + C ) completed 18 units in 18/9 = 2 days [ unitary method]

Total days taken = ( A + B + C ) worked for 2 days + ( B + C ) worked for 2 days + C worked for 3 days = 7 days

Time and work – Alternate day working questions

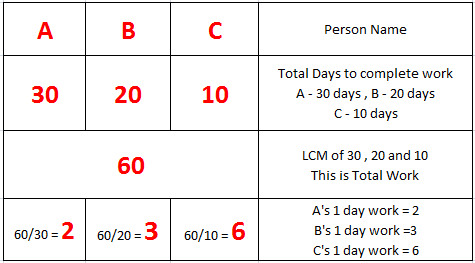
Question ) A can do a piece of work in 30 days , B can do a piece of work in 20 days and C can do a piece of work in 10 days. All three work alternately and B works on first day , A work on 2nd day and C on 3rd day. In how many days the work will be finished if they work together on alternate days in this order ?

Solution : –

Note – Alternate days means no one work together , all work on alternate days.
In these types of question find ( A + B + C ) work together = 2 + 3 + 6 = 11 units but remember this 3 days work of together as all work on alternate days .
B work on 1st day = 3 units
A work on 2nd day = 2 units
C work on 3rd day = 6 units
So in 3 days they together complete = 3 + 2 + 6 = 11 units

Now just divide the total work units by combined ( A+B+C) work and note the remainder
= 60 / 11 = 5 and ( remainder = 5 )
( A + B + C )’s 3 day work = 11 units , so in 15 days they complete – 55 units
Total work left now = 60 – 55 = 5 units [Try to understand this , if not revisit the solution again]
Now its B turn as it work on 1st day which completes – 3 units in a day
Total work left now = 5 – 3 = 2 units
Now its A turn as it work on 2nd day which completes – 2 units in a day
now remaining left units are completed by A.

Total days = 15 days + 1 day + 1 day = 17 days

Traditional Diagram
where B complete 3 units on 1st day , A complete 2 units on 2nd day and C complete 6 unit on 3rd day and so on .

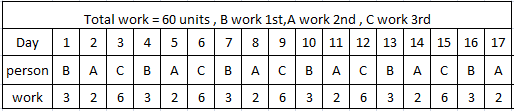
Days wise representation of work by A , B and C

So if we go by this diagram , and calculate total working days it should be equal to 17.

Time and Work – People and work Questions

Question ) 6 men can do a piece of work in 12 days. How many men are needed to do the work in 18 days?
A) 3 men B) 6 men C) 4 men D) 2 men

Solution: Now, if we notice there are multiple people and also along with it multiple amounts of work. Now, this formula will be used.

Note – When work is same , W1 and W2 cancel out each other or taken as 1

$Formula => \frac{M_1 * T_1}{W_1} = \frac{M_2 * T_2}{W_2}$

So,

$\frac{6*12}{1} = \frac{x*18}{1}$

$72 = 18X$

$X=\frac{72}{18}$

$X=4$

Answer: (C) 4 Men

Question) X number of men can finish a piece of work in 30 days. If there were 6 men more, the work could be finished in 10 days less. The original number of men is
A) 10 B) 11 C) 12 D) 15

Solution: Even there are multiple men and multiple amounts of work.
and Work done is same so W1 and W2 cancel out each other.

$Formula => \frac{M_1*T_1}{W_1} = \frac{M_2*T_2}{W_2}$

So,
M1= X , T1=30 , M2=X+6, T2=30-10=20

$\frac{x*30}{1} = \frac{(x+6)(30-10)}{1}$

$x*30 = (x+6)20$

$30x = 20x+120$

$10x = 120$

$x=12$

Answer: (C) 12 Men

Question) 4 men and 3 women finish a job in 6 days, and 5 men and 7 women can do the same job in 4 days. How long will one man and one woman take to do the work?
A) 156/7 days B) 51/2 days C) 58/7 days D) 271/22 days

Solution: There are multiple men and multiple amounts of work. So, you know exactly which formula to be used. Work done is same so W1, W2 and W3 will cancel out each other. The formula to be used is

$\frac{M_1 * T_1}{W_1} = \frac{M_2 * T_2}{W_2}= \frac{M_3 * T_3}{W_3}$

Here,
M1 = 4 men + 3 women , T1 = 6
M2 = 5 men + 7 women , T2 = 4
M3 = 1 men + 1 women , T3 = ? [ to find ]

Equation 1: 4 Men and 3 Women finish a job in 6 days.

$\frac{(4M + 3W)*6}{1} - (1)$

Equation 2: 5 Men and 7 Women can do the same job in 4 days.

$\frac{(5M + 7W) * 4}{1}-(2)$

Equation 3: How long will one and one woman ake to do the work

$\frac{(1M + 1W) * x}{1} -(3)$

Let’s put (1) and (2) together.

$\frac{(4M + 3W) * 6}{1} = \frac{(5M + 7W) * 4}{1}$

$(4M+3W)6 = (5M+7W)4$

$24M+18W = 20M + 28W$

$24M-20M = 28W-18W$

$4M = 10W => M = \frac{10}{4}W = \frac{5}{2}W$

From this we get,

$M = \frac{5}{2}W$

Let’s put (1) & (3) together.

$(4M+3W)6 = (1M+1W) * x$

Now, let’s substitute M as 5/2 W

$(4 * \frac{5}{2} + 3W) 6 = (\frac{5}{2} * W + 1W) * x$

If we reduce it then,

$3W * 6 = \frac{7}{2} * W * x$

$=> x = \frac{2 * 13 * 6}{7} = \frac{156}{7}$

Answer: 156/7 days (A)

Now work is not same in the question.
Question ). 5 men and 3 boys can together cultivate a 23-acre field in 4 days and 3 men and 2 boys together can cultivate a 7-acre field in 2 days. How many boys will be needed together with 7 men, if they have to cultivate a 45-acre field in 6 days?
A) 2 B) 3 C) 4 D) 6

Solution: Here also there are multiple amounts of works and men. But here the work is not same. Below is formula used

$\frac{M_1 * T_1}{W_1} = \frac{M_2 * T_2}{W_2}= \frac{M_3 * T_3}{W_3}$

Here,
M1 = 5 men + 3 boys , T1 = 4 , W1 = 23
M2 = 3 men + 2 boys , T2 = 2 , W2 = 7
M3 = 7 men + X boys [X to find ] , T3 = 6 , W3 = 45

Equation 1: 5 men and 3 boys can together cultivate a 23-acre field in 4 days.

$\frac{(5M+3B) * 4}{23} -(1)$

Equation 2: 3 men and 2 boys can together cultivate a 7-acre field in 2 days.

$\frac{(3M+2B) * 2}{7} -(2)$

Equation 3: How many boys will be needed together with 7 men if they have to cultivate a 45-acre field in 6 days?

$\frac{(7M + xB) * 6}{45}- (3)$

Let’s put (1) = (2)

$\frac{(5M+3B) * 4}{23} = {(3M+2B) * 2}{7}$

After simplifications,

$7(5M+3B) * 4 = 23 (3M+2B) * 2$

After reducing,

$70M + 4B = 69M + 46B$

$M = 4B$

Let’s put (2) = (3).

$\frac{(3M+2B) * 2}{7} = \frac{(7M + xB) * 6}{45}$

After simplifications,

$45(3M+2B) * 2 = 7 (7M+xB) *6After reducing,\[15(3 * 4 B + 2B) = 7 (7 * 4B + xB)$

$15 * 14B = 7 (28 + x)B$

[Taking B as a common in outside]
Aftr reducing

$30 = 28 +x$

$x=2$

Answer: 2 (A)

Work and Contribution Questions

Question) Chandler can do a piece of work in 10 days. Joey can do it in 15 days. If the total wages for the work is Rs. 50. How much should Chandler be paid if they work together for the entire duration of the work?
A) Rs 30 B) Rs 20 C) Rs 50 D) Rs 40

In these types of questions – Divide the total amount by the efficiency of each person.

$1. Effeciency = \frac{Work Done}{Time Taken}$

If work is same then

Efficiency = 1 / Total Time taken = 1 day work

Solution: Let’s find the efficiency of Chandler and Joey.

$E_C = \frac{1}{10}$

$E_J = \frac{1}{15}$

Ration of their efficiency = Chandler Efficiency : Joey Efficiency = 15 :10

Divide the total amount according to the efficiency

Chandler amount =

$= \frac{15}{15 + 10 } * Total Amount$

Chandler amount =

$= \frac{15}{15 + 10 } * 50 = \frac{15}{25 } * 50 = 30$

Joey amount =

$= \frac{10}{15 + 10 } * 50 = \frac{10}{25 } * 50 = 20$

Answer: Rs.30 (A)

Question ) Gabbar and Mogambo together can do a piece of work in 7 days. If Gabbar does twice as much work as Mogambo in a given time, how long will Gabbar alone take to do the work?
A) 6.33 days B) 10.5 days C) 11 days D) 72 days

Solution: Gabbar and Moagambo together can work for 7 days.
Gabbar can do twice work than mugambo, so
Gabbar Efficiency : Mogambo Efficiency = 2 : 1
Efficiency = 1 day work
Gabbar 1 day work : Mogambo 1 day work = 2 : 1
( Gabbar + mogambo ) 1 day work = 1 /7 [ Given in question]
Now divide the the 1 day work wrt to efficiency
Gabbar share = [ 2 /3 ]* 1/7 =

Gabbar_1 day work = $\frac{Gabbar share}{Gabbar + mogambo share}$ * Total 1 day work

Gabbar_1 day work = $\frac{2}{3} * \frac{1}{7}$

Gabbar 1 day work = 2 / 21
Gabbar can do total work in 21/2 days = 10.5 days

Some one left the work – Questions

Question ) A can do a piece of work in 20 days. He works at it for 5 days and then B finishes it in 10 more days. In how many days will A and B together finish the work?
A) 8 days B) 10 days C) 12 days D) 6 days

Solution: In these types of questions – Simply assume Total work 20 units
A can do 20 Units in 20 days.
In 5 days A can do 5 units of work.
Remaining work = 20 – 5 = 15 units
These 15 units completed by B in 10 days.
So , 1 unit is completed by B in 10/15 days
20 units is completed in [10/15] * 20 = 40 / 3 days
B can do 20 units in 40/3 days

A’s 1 day work = 1/20
B’s 1 day work= 3/40
(A + B)’s 1 day = 1/20 + 3/40 = 5/40 = 1/8
A and B can do complete work in 8 days

Answer: 8 Days (A)

Question ) Louis can do a piece of work in 25 days and Clark can do it in 20 days. They work for 5 days and then Louis goes away. In how many more days will Clark finish the work?
A) 10 days B) 12 days C) 14 days D) 11 days

Using padhle LCM method

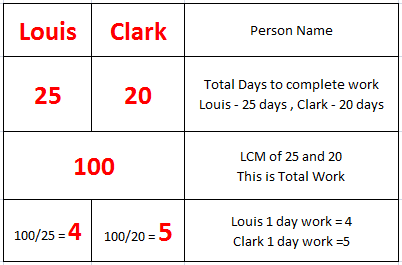
( Louis + Clark ) 1 day work = 4 + 5 = 9
Louis and Clark together work in 5 days = 9 * 5 = 45
Remaining work = total work – work done in 5 days = 100 – 45 = 55

Clark 1 day work = 5 units
Clark can do remaining 55 units in 55 / 5 = 11 days
Answer = 11 days (D)

Answer: 10.5 Days (B)

Join Telegram for Updates