Distance and time is one of the common topic and always be a part of exams like SSC CGL, CHSL , SBI PO, SBI clerk etc. In this post , we will learn about speed, time and distance. Speed can be either in KM/H or M/S. He is travelling in 50 Km/h. Distance means the distance covered. It can be in metres or in Kilometres. Time is the time taken to travel a distance. She took 1 Hr to complete her journey. Time can be indicated in the form of seconds, minutes, hours, days, weeks, months and also years.
Table of content
1) Relative Speed concept
2) Problem on Trains concept and short trick
3) Speed , Distance and Time basic formula
4) Basic conversion Units of speed
5) Basic question of Speed , Distance and Time
6) Advance question of Speed , Distance and Time
Before understanding distance , time and speed concepts we need to understand the concept of relative speed.
Relative speed concept
Relative speed – The speed of one object with respect to other object.
1) If two bodies moving in same direction , their relative speed is difference of speed of both objects.
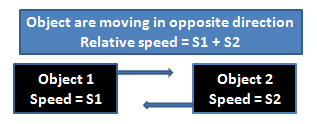
2) If two bodies moving in opposite direction , their relative speed is addition of speed of both objects.

Problem on Trains concept and short trick
We will learn about all the train related question here out. Before we step into some questions. Let’s learn some basic formulae.
Basic formula of Speed , Time and Distance
Let us do some case studies.
Case 1
When two trains are travelling in the opposite direction what is the distance, speed, and time traveled moving across each other?
Solution:
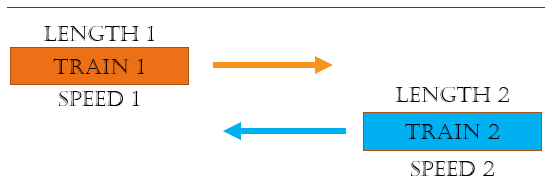
= Sum of the length of the trains =
= Sum of both the speed of the trains =
Case 2
When two trains are travelling in the same direction what is the distance, speed, and time traveled moving across each other?
Solution:
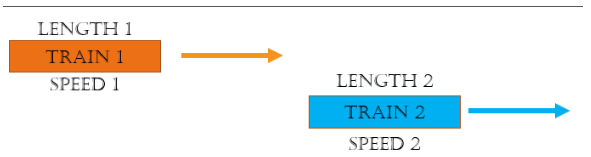
= Sum of the length of the trains =
= Difference of the speed of the trains =
Case 3
What is the time, distance and speed when a train travels through a tunnel, bridge or platform?
Solution:
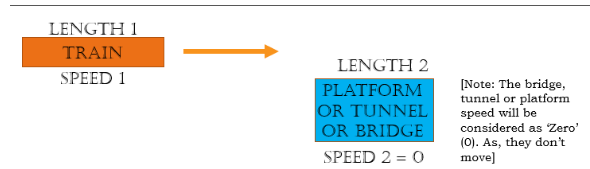
= Sum of the length of the trains =
= Difference of the speed of the trains =
Case 4
What is the time, distance and speed when a train crosses a human/stationary object moving in the opposite direction?
Solution:
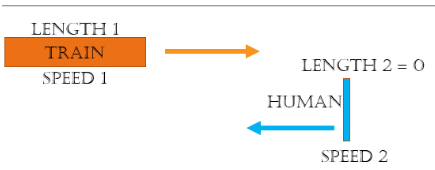
Note – The length of the human will be zero (0) as the length of the human is negligible as compared to the train, So there is no L2.
= Sum of the length of the trains =
= Sum of the speed of the trains =
Case 5
What is the time, distance and speed when a train crosses a human moving in the same direction?
Solution:
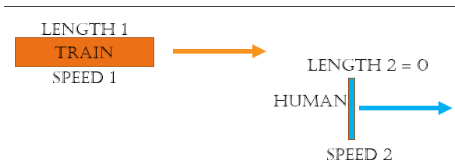
Note – The length of the human will be zero (0) as the length of the human is negligible as compared to the train, So there is no L2.
= Sum of the length of the trains =
= Difference of the speed of the trains =
Case 6
What is the time, distance and speed when a train crosses a stationary pole/object?
Solution:
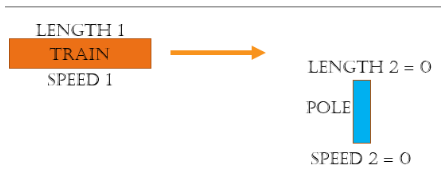
Note – The length of the human will be zero (0) as the length of the human is negligible as compared to the train, So there is no L2.
= Sum of the length of the trains =
= Difference of the speed of the trains =
Can anyone say the formula for Average speed?
Solution: Check below , we all know that
Basic conversion Units of speed
There are two basic units we must know while solving the train questions.
1) Converting Km/Hr to M/S
2) Converting M/S to Km/Hr
Get into explanation now
1 Km = 1000 metre
1 hour = 3600 seconds
So , 1 Km/hr = 1000 metre / 3600 seconds = 5 / 18 m/s
Similarly if we reciprocate the above
1 m/s = 18/5 km/hr
Basic distance,time and speed questions
Question 1 ) The Hogwarts Express travels 650 km in 5 hours and another 940 km in 10 hours. What is the average speed of the train?
A) 112 kmph B) 168 kmph C) 106 kmph D) 126 kmph
Solution: We are asked to find the average speed of the Hogwarts Express.
We all know that
Note: The distance is given in Km/Hr. and Time is also given in Hours. So, there were no further calculations. If question demands a conversion from Km/Hr. TO M/S means we ought to do it.
Answer: 106 Km/Hr.
Problem on Trains question
Question 2) . Two trains having lengths of 140 m and 160 m run at the speeds of 60 km/hr and 40 km/hr respectively in opposite directions (on parallel tracks). The time which they take to cross each other is
A) 3 sec B) 9.8 sec C) 54 sec D) 10.8 sec
Solution: This question is an example of Case Study 1. And Padhle can hear you saying the formula correct. Let us solve the question.
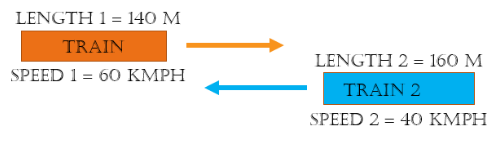
L1 = 140 m , L2 = 160 M
now speed is in Km/h and we have to find the answer in seconds as given in the option, So we convert km/h to m/s.
S1 = 60 Km/h , S2 = 40 Km/h
Note : Sum of speed is multiplied by 5/18 to convert speed from Km/hr to metre/sec .The length of the train is given in Metres but the speed is given in KMPH. So, to get the correct answer we need to convert any of these to get the correct answer. Options are given in seconds. So, it is better to convert the KMPH to M/S. So only speed is getting converted to M/S.
Answer = 10.8 Seconds
Question 3) A train 125 m long passes a man, running at 5 km/hr in the same direction in which the train is going, in 10 seconds. The speed of the train is:
A) 45 kmph B) 50 kmph C) 40 kmph D) 55 kmph
Solution: This question refers to the case study number 5.
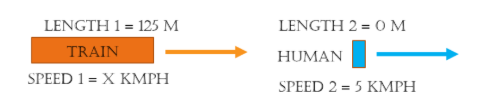
we need to find the answer in Km/hr , so convert all values in Km and hours
L1 = 125 m = 125 /1000 = 0.125 Km
Speed 2 = 5 km/hr and Let say Speed 1 = X km/hr
Time taken to pass a man = 10 sec = 10/3600 hrs = 1/360
Given, Time ( Train crossed a man ) = 1/360 hrs =>
Let’s bring X – 5 to the LHS. So,
Solving above equation
X = 45 +5
X = 50 KMPH
Answer: (B) 50 KMPH
Question 4) The length of the bridge, which a train 130 metres long and travelling at 45 km/hr can cross in 30 seconds, is:
A) 200 m B) 225 m C) 245 m D) 250 m
Solution: The formula of Case study 3 will be applied.

we need to find the answer in Metre , so convert all values in metre and seconds
L1 = 130 m and Let say L2 = X m
Speed 1 = 45 km/hr = 45 * (5/18) = 12.5 m/sec
Time taken to cross a bridge = 30 sec
Answer: (C) 245 m
Question 5) A train crosses a man in 9 seconds. The same train crosses a 240-metre-long platform in 24 seconds. What is the time taken by the train to cross another train of 256 m length moving at 12 m/sec in the same direction?
A) 16 sec B) 50 sec C) 144 sec D) 100 sec
Solution:
Let us create the equation when the train crosses the man.
T = Time taken by train to cross a man
D = Distance( Length of train) and S = Speed of train
Case study 6
Note : The distance is anyway the length of the train so only D has been denoted as L.
Let us create another equation when the train crosses a 240 metre length platform in 24 seconds.
Case 3 Study
T = Time taken by train to cross platform
L1=Length of train and S = Speed of train
Put (1) equation in (2) together [ L = 9S ]
Now put (3) in (1) to get the length of the train
Now, we got the length of the train.
Let us find the actual question of how much time will the train take to cross another train of 256 which is moving at 12 M/S in the same direction.
Case study 2
L1 = 144 m , L2 = 256 m , S1 = 16 m/s , S2 = 12 m/s
Answer: (D) 100 Seconds
Time and Distance Advance Level Questions
Question 1 ). The Alpha Express left Pune for Mumbai at noon sharp. Two hours later, the Deccan Queen started from Pune in the same direction. The Deccan Queen overtook the Alpha Express at 8 p.m. Find the average speed of the two trains over the journey if the sum of their average speeds is 70 kmph.
A) 35 kmph B) 34.28 kmph C) 50 kmph D) 12 kmph
Solution:
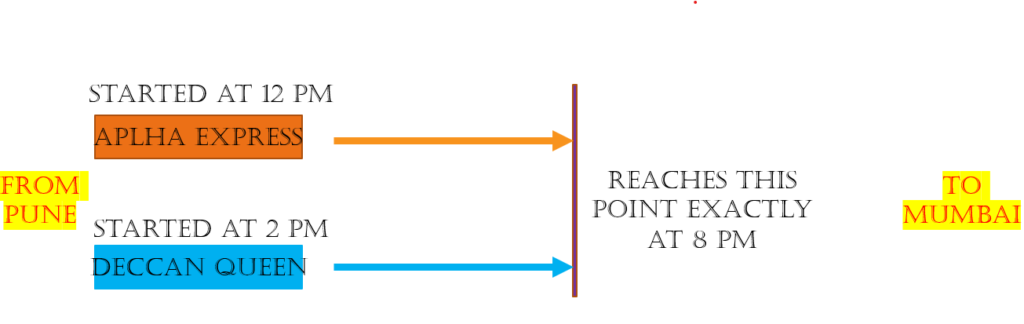
The distance from Pune to Mumbai is going to same for Aplha Express and Deccan Queen. So,
Also given, the average speed of both the trains is 70
So, let us denote Time by ‘T’, Speed by ‘S’, and Distance ‘D’.
Formula for Distance = Speed * Time
Now, how much time did Alpha took to reach the point when Deccan crossed it?.
Yeah, Correct it took 8 hours. While Deccan took 6 hours.
So,
We know that if one speed is
If total speed is 70 KMPH and then One of the speeds is 30 KMPH then other should be
We need to find the average speed.
Important Note :
There is a special formula to find the average speed when the distance is same. Now, here the distance is same from Pune to Mumbai.
The formula is
Now let us substitute the items in the special formula.
Answer : (B) 34.28 KMPH
Question 2 ) Two trains for Mumbai leave Delhi at 6 a.m. and 6:45 a.m. and travel at 100 kmph and 136 kmph respectively. How many kilometres from Delhi will the two trains be together?
A) 272 km B) 260 km C) 283.33 km D) 262.4 km
Solution: Here also distance of both the train is the same when they meet together as they start from same point. The formula for Distance = Speed * Time
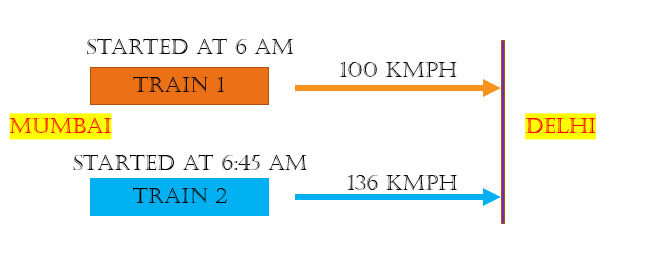
Distance traveled by both trains is same.
Let say Time taken by Train 1 to reach common point is T1 = T hours, So
Time taken by Train 2 to reach common point is T2 = T – 45 minutes .
Note – [ Train 2 starts 45 mins later than Train 1 ]
Now we have to find answer in Km and hours ,so convert all values to Km and hours , so
T2 = T – 45 /60 hours = T – 3/4 hours
We found out the time, now we need to find the distance.
Distance traveled by Train 1 , Speed of Train 1 = 100 Km/hr
Time taken = 17/6 hours
Distance traveled by Train 1 = Distance traveled by Train 2 = 288.33 Km/hr
Answer: (C) 288.33 KMPH
Question 3) Lonavala and Khandala are two stations 600km apart. A train starts from Lonavala and moves towards Khandala at the rate of 25km/h. After 2 hours, another train starts from Khandala at the rate of 35km/h. How far from Lonavala will they cross each other?
A) 250 km B) 300 km C) 279.166 km D) 475 km
Solution: Here, the distance is the same between the station of Lonawala and Khandala which is 600 KM apart.
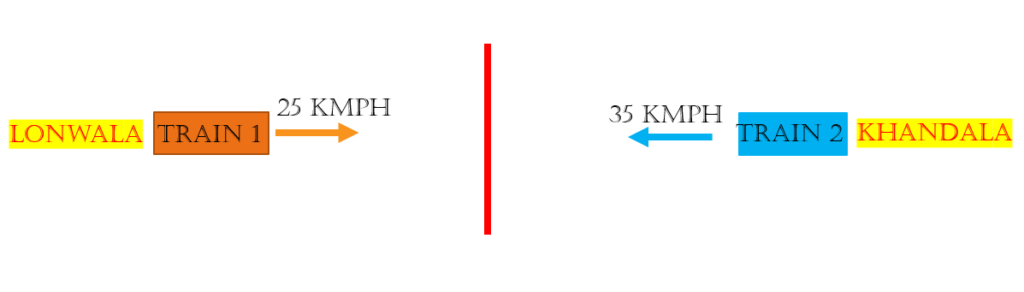
Time taken by Train 1 to cross each other is T hour
Time taken by Train 2 to cross each other is T – 2 hour [ Train 2 starts 2 hour later than Train 1 ]
The distance between the stations = 600
The formula for Distance = Speed * Time taken
Distance from lonavala where train meets = Distance traveled by train 1
Answer = (C) 279.166 KM
Question 4 ) A & B are traveling from X to Y. A starts at 12 pm at a speed of 63 mph. B starts at 1:30 pm at a speed of 84 mph. At what time will A be 34 miles ahead of B?
A) 4:22:51 pm B) 4:42:51 pm C) 4:32:51 pm D) 4:38:51 pm
Solution:
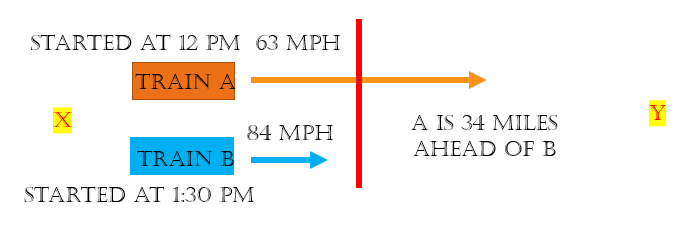
Time Taken By A when A is 34 miles ahead of B is T hours
Time Taken By B when A is 34 miles ahead of B is T – 1.5 hours
[B starts 1.5 later than A]
The train A is 34 miles ahead of B.
The formula for Distance = Speed * Time.
In order to 4. 38 hrs into minutes lets multiply .38 with 60.
Answer: (A) 4:22:51
Question 5) Walking at 3/4 of his normal speed, Gandalf is 16 minutes late reaching his office. The usual time taken by him to cover the distance between his home and his office is
A) 48 minutes B) 60 minutes C) 42 minutes D) 62 minutes
Solution: The distance between the office and home is constant.
At normal/Usual days
Distance = D , Speed = S , Time Taken = T
At that day
Distance = D , Speed = 3/4 S [ 3/4 normal speed] , Time Taken = T + 16 [ 16 minute late]
If he gets late while walking 3/4th of the speed then the normal speed will be higher be more than that of 3/4th of his normal speed. So, 16 is added.
Both the S gets cancelled.
So,
Answer: (A) 48 Minutes
Question 6) Sam and Frodo travel the same distance at the rate of 6 km per hour and 10 km per hour respectively. If Sam takes 30 minutes longer than Frodo, the distance traveled by each is:
A) 6 km B) 10 km C) 7.5 km D) 20 km
Solution:
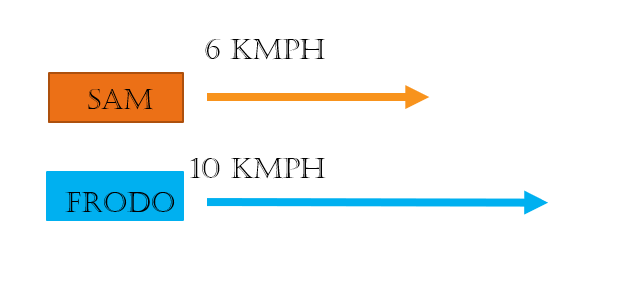
The distance traveled is same between Sam and Frodo as mentioned in the question.
The distance traveled = Speed*Time
Question 7) Flash and Quicksilver are 90 km away from one another. They are starting to move towards each other simultaneously, Flash at a speed of 10 kmph and Quicksilver at a speed of 5 kmph. If after every hour they double their speeds, what is the distance that Flash will travel until he meets Quicksilver?
A) 45 km B) 60 km C) 30 km D) 80 km
Solution: Let’s solve the above question with the help of ratio.
Note: Always remember when the distance is constant the ratio of the two speeds also stays constant. As happened in the above question.
Flash starts at 10 KMPH and Quicksilver with 5 KMPH.
So, ratio = 10 : 5 = 1 : 2.
After one hour, the speed becomes 20 KMPH and 10 KPH respectively.
So, ratio stands = 20 : 10 = 1 : 2.
Hence proved that when the distance is constant then the ratio also tends to be constant.
Here the ratio is 1 : 2.
Make 90 KM to be divided among the ratio of 1 : 2.
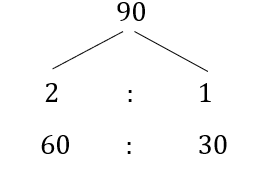
The distance covered by Flash until he meets Quicksilver is 60 KM
Answer: (B) 60 KM
Practice some Distance , time and speed question
Practice some Problem on trains question
Join our telegram channel for latest updates.
For any queries , mention in comments.