Shortcut tricks on Profit and Loss – Solve questions in seconds

Profit and Loss are most asked and appearing questions in aptitude and government papers. Everyone is aware of profit and loss.
Profit = Selling price is greater than the Cost price.
Loss = Cost price is greater than the Selling price.

Cost Price – Price at which item is bought.
Selling Price – Price at which item is sold.
Marked Price – Price marked on Item – Marked Price may or may not equal to Selling Price.
Loss – when Cost price is greater than Selling Price.
Profit – when Selling price is greater than Cost Price.

Table of Content
1) Formula – Profit and Loss
2) Basic Profit and Loss Question
3) Successive Discount Questions

Important Profit and Loss Formula

Gain price = Selling Price (SP) – Cost Price (CP)
Loss price = Cost Price (CP)- Selling Price (SP)

$1. Gain Percentage = \frac{Gain Price}{Cost Price} * 100$

$2. Loss Percentage = \frac{Loss Price}{Cost Price} * 100$

$3. Gain/Loss Percentage = \frac{SP - CP}{CP}*100$

Golden Formula to find CP and SP

In Case of Profit – > CP * [ 100 + Profit % ] = SP * 100
In Case of Loss – > CP * [ 100 – Loss % ] = SP * 100

Note – C.P. is always 100 percent of it self.

Scenario to find the SP and CP if the gain is 10%

$1. SP = \frac{110}{100}*CP$

$2. CP = \frac{100}{110}*SP$

Scenario to find the find the SP and CP if the loss is 10%

$1. SP = \frac{90}{100}*CP$

$2. CP = \frac{100}{90}*SP$

Important note:
1. In order to find the SP, the denominator should always be 100
2. In order to find the CP, the numerator should always be 100

Basic Profit and Loss Questions

Question 1 ) Steve buys an old scooter for Rs. 4700 and spends Rs. 800 on its repairs. If he sells the scooter for Rs. 5800, his gain percent is?

Solution: Given,

$CP = 4700 + 800 = 5500$

$SP = 5800$

We know that in case of Gain –

$Gain\Loss Percent = \frac{SP - CP}{CP} * 100$

$Gain\Loss Percent = \frac{5800 - 5500}{5500} * 100$

$Gain\Loss Percent = \frac{300}{5500} * 100$

$Gain\Loss Percent = 5.4545$

Answer = 5.4545%

Question 2 ) The CP, when SP is Rs.40.60 and gain 16% is ?

Solution: We are supposed to find the CP. We know that when we are supposed to find the CP, the numerator is always 100.
Given,
SP = 40.60 , Gain % = 16
Use this formula –

CP * 116 = 100 * 40.60

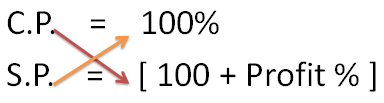
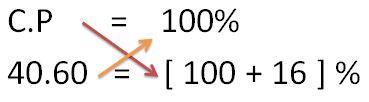
$CP = \frac{100}{116}*40.60$

The denominator is 116 because there is a gain % of 16

$CP = 34.9$

Answer: 34.9

Question 3 ) By selling 33 metres of cloth, one gains the SP of 11 metres. Find the gain percent?

Solution: Let’s assume the SP of 1 Metre = x
Then, SP = 33x (Selling 33 metres)
The Gain = SP of 11 = 11x (by selling 33 metres he gains the SP of 11 metres)
In order to find the gain %, we need to know the CP
CP = SP – Gain

$CP = 33x - 11x = 22x$

$Gain Percent = \frac{11x}{22x}*100$

$Gain Percent = 50$

Answer: 50%

Question 4 )A shopkeeper marks all his goods at 50% above CP & offers a discount of 25% on the marked price. What is his actual profit price?

Solution: Whenever we are supposed to assume a number. It is always better to assume 100.
Let’s assume CP = 100
MP = 150 (50% above CP)

$SP = 150 - 150*\frac{25}{100}$

Discount is being offered at 25% on MP.
SP = 112.5
Actual Price = 112.5 – 100 = 12.5

Answer: 12.5

Question 5 ) In a certain store, the profit is 320% of the cost. If the cost increases by 25% but the SP remains constant, approximately what percent selling price is the profit?

Solution: Here also we need to assume a number so that we can find out the CP and Sp.
Let’s assume that CP = 100.

$SP = 100 + \frac{320}{100}*100$

SP = 420
(320 % on 100 – which is CP)
CP increases by 25%

$New CP = 100 + \frac{25}{100}*100$

New CP = 125

$Gain Percent = \frac{420-125}{420}*100 = 75$

We are dividing it by 420 because we are asked to find what percent of selling price is the profit.
Gain percent on SP = 70.2

Answer: 70.2

Question 6 )An object is sold for Rs.150 making a profit of 50% on the SP. If the article is bought Rs.25 less, what price must be marked so as to gain 40% by selling the object at market price?

Solution: Given, SP = 150.
Profit = 50% on SP =

$Profit = \frac{50}{100}*150 = 75$

CP = SP – Profit = 150 – 75 = 75

New CP = 75 – 25 = 50 ( If the article is bought for Rs.25 less )
MP = 50 + 40% on 50 [ 40% gain on Marked price ]

$MP = 50 + \frac{40}{100} * 50$

MP = 70

Answer: 70

Question 7 ) Joey has 12 eggs with him. He sells x at a profit of 10% & remaining at a loss of 10%. He gains 5% on whole. What is the value of x?

Solution: He sold some eggs (x) at 10% gain and remaining (12-x) at a 10% loss and overall gain is 5 %.
10 % gain on x eggs + 10% loss on (12-x) eggs = overall 5% gain on 12 eggs
Understand the above equation carefully

$x*\frac{110}{100} + (12-x) \frac{90}{100} = 12*\frac{105}{100}$

All the 100 in the denominator gets cancelled

$110x + 12*90 - 90x = 12 * 105$

$30x + 12 * 90 = 12 * 105$

$20x = 12 (105-90)$

$20x = 12 (15)$

$20x = 180$

$x = \frac{180}{20}$

$x = 9$

Answer: 9

Question 8 ) In a market, the price of medium quality mangoes is half of that good quality mangoes. A shopkeeper buys 80 kg good quality mangoes and 40 kg medium quality mangoes from the market and sells them at a common price, which is 10% less than the price he bought the good quality ones. His overall profit is?

Solution: Given
let say – Price of good quality per Kg = 100
And Price of medium quality per Kg = 50 [ half of good quality mangoes ]
He buys 80 kg good quality and 40 kg of medium quality,
Hence total cost price of mangoes is –

$CP = 80*100 + 40*50 = 10000$

He sells all 120 kg in 10% less than good quality ones.

$SP = 100 - \frac{10}{100} * 100 = 90$

SP = Rs 90 per Kg –
For 120 Kg S.P. is

$SP = 120*90 = 10800$

Hence Final CP of all mangoes = 10000
SP of all mangoes = 10800

$Gain Percent = \frac{10800 - 10000}{10000} * 100$

$Gain Percent = 8$

Answer: 8%

Question 9 ) If the CP of 48 articles is equal to the SP of 32 articles, then what is the profit%?

Solution: Given,
CP of 48 Articles = SP of 32 Articles
If CP of 1 Article = 100
Then,
SP of 32 Articles = 4800 (CP of 48 Articles is equal to the SP of 32 Articles)
CP of 32 Articles = 3200
Profit = 4800 – 3200 = 1600

$Profit Percent = \frac{1600}{3200}*100 = 50$

Profit = 50%

Answer: 50%

Question 10 ) By selling 90 pens to Rs. 80 a man loses 20%. What should be SP (Rs.) of 90 pens for 20% profit?

Solution: Given,
SP of 90 pens = Rs. 80 (Loss of 20%)
SP = 80 , Loss % = 20

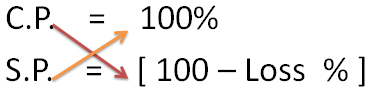
Put value in above equation –

Cross multiply
CP * 80 % = 80* 100 %

$80*CP = 100*SP ----- (1)$

Giving SP = Rs.80 in (1)

$80*CP = 100*80$

80 gets cancelled
CP = 100.
We are actually supposed to find the SP on the CP. We need to find the profit if the profit percent is 20.
Again use the same formula –
CP = 100
Gain percent = 20

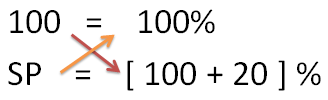
Cross multiply

$120*CP = SP * 100----- (2)$

Substitute CP = 100 in (2)

$120*100 = SP*100$

100 gets cancelled
SP = 120

Answer: 120

Question 11 ) A trader buys 800 kgs of tomatoes for Rs. 7200. 10% of tomatoes are damaged during transportation. At what rate (Rs/Kg) should he sell the rest to earn 30% of profit?

Solution: Given,
800 kg = 7200
10% of rotten tomatoes = 80 kg (10% of 800 kg)
720 kg = 7200
In order to find the CP per kg

$CP per kg = \frac{7200}{720} = 10$

CP = 10
SP = 13 (10+30% profit)
SP = 130% of CP = 13
SP = 13

Answer: 13

Successive Discount Questions

In order to find the net discount in the case of successive discount
Net discount = a + b – (a*b)/100
a = First successive discount
b = Second successive discount
This formula is applicable only for the two successive discounts

Golden formula to find MP and SP

Note – Marked Price is always 100 percent .

Question 12 ) After two consecutive discount of 20% & 35%, an article is sold for Rs. 50,700. What is the MP of the article?

Solution: Let us take the first discount and the second discount as 20% and 35% respectively.

$Net discount = a + b - \frac{20*35}{100}$

a = 20 ; b =35

$Net discount = 20 + 35 - \frac{20*35}{100} = 20 + 35 - 7 = 48$

Net Discount = 48%
SP = 50700 [ given ]

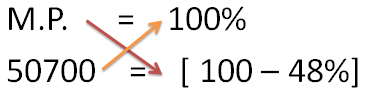
SP = 52 (100 – Net discount which is 48)
Cross multiply

$52*MP = SP * 100$

We are supposed to find the MP
We know that SP = 50,700

$52*MP = 50,700*100$

Taking 52 to the other side

$MP = \frac{50,700*100}{52} = 97500$

Answer: 97,500

Question 13 ) What is the net discount of 20%, 10% and 30%?

Solution: D1 = 20%, D2 = 10% and D3 = 30%
Let’s use the net discount formula

$Net Discount = a+b - \frac{a*b}{100}$

If we take D1 = 20 and D2 = 10,
a = 20, b = 10

$Net Discount = 20+10-\frac{20*10}{100} = 20+10-2 = 28$

This net discount becomes the new D1 and D3 becomes D2.
Now, D1 = 28 and D3 = 30 are taken into consideration

$Net Discount = 28+30-\frac{28*30}{100} =28+30 - 8.4 = 49.6$

Net discount of all the three discount = 49.6

Answer: 49.6

New net discount is taken into consideration as D1 until the last discount is not taken as D2 for more than 2 successive discounts as shown above.

Question 14 ) A shopkeeper by selling 5 items earns a profit to the selling price of 1 item. What is his profit percentage?

Solution: Given
Let say SP of 1 item = 100
SP of 5 item = 100*5 = 500
Profit = SP of 1 item = 100
CP = SP – Profit = 500 – 100 = 400

$Profit percent = \frac{100}{400}*100 = 25$

Profit = 25%

Answer: 25%

Question 15 )A dishonest dealer professes to sell his goods at CP but uses the weight of 875 gm for the kilogram. His gain percent in percentage is?

Solution: Given
1 kg = 875 gm
CP of 1000 g = 1000
SP of 1000 g = 1000 (The dealer is selling at the CP)
The dealer is selling 875 gm at 1000
CP of 875 gm = 875
SP of 875 gm = 1000
Profit = SP – CP = 1000 – 875 = 125

$Profit Percent = \{frac{125}{875}*100 = 14.28$