In this article , definitely be the end of this article you will learn all concepts of percentages and tricks to solve questions within seconds to save time during exams like SSC CGL , Bank PO , CHSL , IBPS clerk , SBI clerk , CAT and other competitive examinations
Table of content
1) Percentage explanation and split method
2) Change in Percentage concept
3) Mixture with percent questions
4) Population and percentage questions
5) Complex percentage questions
6) All video of percentage concepts
What is percentage ?
A percentage means “By a hundred” is a number or ratio expressed as a fraction of 100. Percent is denoted by % symbol.
For example:
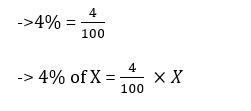
Can someone say 78 % of 200 ?
Got stuck?
Traditional Way
78 % of 200 means 78 /100 * 200 = 156
Tricky padhle way
Before we jump into the tricks remember the below following logic
100 % = 100 / 100 = 1
50 % = 50 / 100 = 1/2
25 % = 25/ 100 = 1/4
10 % = 10/100 = 1/10
5% = 5/100 = 1 /20
1% = 1/100
To get the percent of a complex number – we should split our number into the above table. Its all up to how you want to split.
1st approach to split –
78 % = 50% + 25 % + 1% + 1% + 1%
Let us add 50% of 200 + 25% of 200 + 1 % of 200 + 1 % of 200 + 1 % of 200.
78% of 200 = 50% of 200 + 25% of 200 + 1% of 200 + 1% of 200 + 1% of 200
78% of 200 = 50% * 200 + 25% * 200 + 1% * 200 + 1% * 200 + 1% * 200
78% of 200 = 1/2 * 200 + 1/4 * 200 + 1/100 * 200 + 1/100 * 200 + 1/100 * 200
78% of 200 = 100 + 50 + 2 + 2 + 2 = 156
2nd approach to split
78 % = 50% + 10% + 10% + 5% + 3%
Let us add 50% of 200 + 10% of 200 + 10 % of 200 + 5 % of 200 + 3 % of 200.
78% of 200 = 1/2 * 200 + 1/10 * 200 + 1/10 * 200 + 1/20 * 200 + 3/100 * 200
78% of 200 = 100 + 20 + 20 + 10 + 6 = 156
We found the answer without any calculator.
The basic is breaking down. Break down the question and get the answer within seconds.
Note – Use split method based on your easiness.
Below is you tube video explaining all concepts
Percentage Type of questions maximum deals with all the examinations.
Change in Percentage concept and tricks
There is one golden formula to solve the questions for change in percent

Note –
1) If new value is more than initial value , change is always positive.
2) If new value is less than initial value , change is always negative.
Let us not eat your time. Let us proceed to the samples.
Sample 1
Solution:

Let us go through the golden formula
Beginning value is considered as Base value
End value is considered as New value

Ans: 20% is the change from 50 to 60
Sample 2

Solution: Beginning value will be considered as base value and end value will be considered as new value.
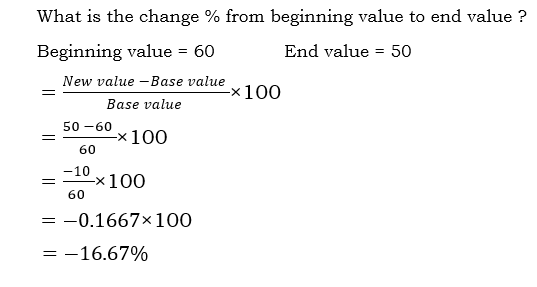
Ans: – 16.67 % of change from 60 to 50.
Let us solve some interesting questions.
Question ) A batsman scored 120 runs which included 3 boundaries and 8 sixes. What % of his total score did he make by running between wickets?
Solution:
Total runs made = 120
Runs made in boundaries = 3 * 4 = 12 (The batsman hit 3 boundaries. One boundary is equal to 4 runs)
Runs made in sixes = 8 * 6 = 48 (The batsman hit 8 sixes. One six is equal to 6 runs)
Total runs made in boundaries and sixes = 12 + 48 = 60.
Runs remaining = 120 – 60 = 60
60 runs made running between the wickets.
Now, let us go through the golden formula
Here the total runs made is beginning value = 120
Runs made in running between the wickets = 60
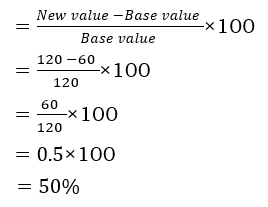
Ans: 50% runs he made in running between the wickets.
Mixtures and Percentage questions
Now, the following formula is to find out how many percent one liquid is on other liquid.
Concept – Suppose we have mixture of any entity – X + Y + Z
Percent of X = X / X+Y+Z
Percent of Y = Y / X+Y+Z
Percent of Z = Z / X+Y+Z
For example, let us take 9 litres of water and 16 litres of milk.
What is the percentage of milk if 9 litres of water and 16 litres of milk is mixed?
Solution: The total number of litre of mixture = 16 litres of milk + 9 litres of water = 25 litres.
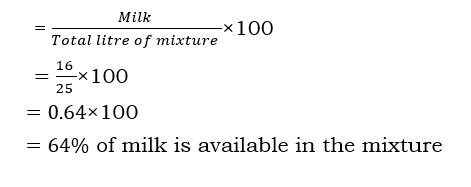
For the same question, what is the percentage of water in the mixture?
Solution:
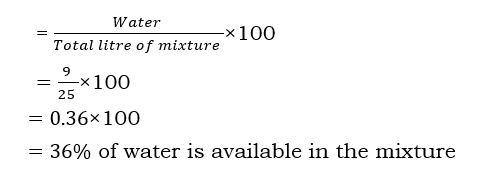
Let us solve, another example.
Question ) A mixture of 30 litres of milk and water contains 20% of water. A new mixture is formed by adding 5 litres of water. What is the percentage of milk in the new mixture?
Solution:
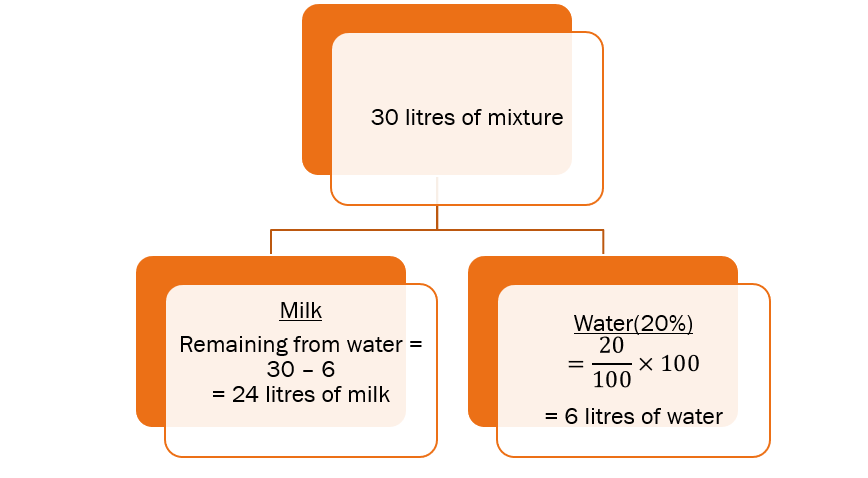
Total mixture – 30 litres
Total Water -> 20% of total mixture = 20% of 30 = 6 litres
Total Milk -> Total mixture – Total water = 30 – 6 = 24 litres
Now, 5 litres of water is added.
Total NEW mixture -> 30 + 5 = 35 litres
Total Water in new mixture -> 6 + 5 = 11 litres
Total Milk in new mixture -> Total mixture – Total water = 35 – 11 = 24 litres

Now, the question is to find the percentage of milk in the new mixture.

Ans: 68.57% of milk is available in the mixture.
Trick to get new value on increment and decrement
Problem ) A number 100 is increased by 10% . What will the new value ?
Trick – A number is 100% of itself
New percent is 10 percent more,
New percent is = 100% + 10% = 110%
New number is = 110% * 100 = 110/100 * 100 = 110
Problem ) A number 100 is decreased by 10% . What will the new value ?
Trick – A number is 100% of itself
New percent is 10 percent less ,
New percent is = 100% – 10% = 90%
New number is = 90% * 100 = 90/100 * 100 = 90
Try to understand this trick again if not understood.
Population percentage question
Let us solve some population questions.
Question 1 ) The population of the town is 10,000. It increases annually 20% p.a. What will be the population after 2 years?
Solution:
The population increases annually,so we will add here
Initial population – 10,000
Population after 1 year = 10,000 + 20% of 10,000
= 10000 + 2000 = 12,000
Now population – 12,000
Trick – total new percent = 100% + 20% = 120%
New population = 120% of 10,000 = 12,000
Population after 2nd year = 12,000 + 20% of 12,000
= 12,000 + 2,400 = 14,400
Trick – total new percent = 100% + 20% = 120%
New population – 120% of 12,000 = 14,400
Answer: 14,400 after two years
Question 2 ) The population of a town is 8,000. It decreases annually by 20% p.a. What will be the population after 2 years?
Solution:
The population decrease annually, so we will subtract here
Initial population = 8,000
Population after 1 year = 8,000 – 20% of 8,000
= 8,000 – 1,600= 6,400
Now population – 6,400
Trick – total new percent = 100% – 20% = 80%
New population = 80% of 8,000 = 6,400
Population after 2nd year = 6,400 + 20% of 6,400
= 6,400 + 1,280 = 4,120
Trick – total new percent = 100% – 20% = 80%
New population = 80% of 6,400 = 4,120
Answer: 4,120 is the population after two years.
The above questions can be solved by simple interest method or consecutive discount of profit and loss also.
Complex percentage questions
Let us try some other types of sums.
Note – when all the value are given in percent , then always take the base value as 100.
Question ) When a number is increased by 10% and then reduced by 10% of that same number, What is the change from starting number?
Solution: Whenever a question is raised without setting a number. It is always better to take the number as 100 as shown in the pic below.
Take starting number = 100
After 10% increment
new number = 100 + 10% of 100 = 100 + 10 = 110
Trick – A number is 100% of itself.
Increment percent – 10%
New total percent – 100% + 10% = 110%
New number – 110/100 * 100 = 110
Now after 10% decrement
New number = 110
new number = 110 – 10% of 110 = 110 – 11 = 99
Trick – A number is 100% of itself.
Decrement percent – 10%
New total percent – 100% – 10% = 90%
New number – 90/100 * 110 = 99
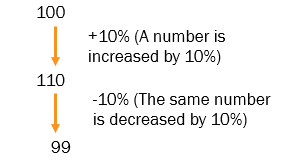
We assumed that 100 is the starting number. The end answer is 99.
So, the change from the starting value to the end value is
Start Value – 100
End value – 99
Change in percent = [ 99 – 100 / 100 ] * 100 % = [-1/100] * 100
= – 1 %.
Question ) If X and Y are 20 % and 25 % greater than Z respectively. By how much % is X smaller than Y?
Solution:
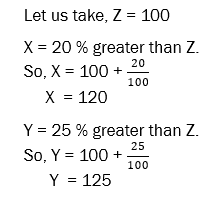
Now, the question asks us to find out how much % is X smaller than Y. Here, we need to apply the golden formula of change % taking X as base value and Y as new value and compute the change in %.
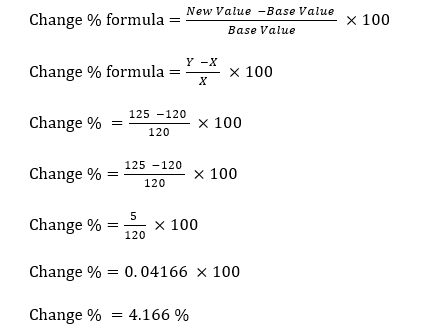
Question ) 5% of A’s income is equal to 15% of B’s income & 10% income of B’s income is equal to 20% of C’s income. If the income of C is 2,000 then the total income of A, B and C?
Solution:

Answer: The total value of all the three earning together is 18,000.
Question ) In an examination it is required to get a minimum of 30% of total marks to pass. A student got 110 marks and was declared fail by 10 marks. What is the total marks for the examination?
Solution:
To pass the required marks = 110 [Student’s marks] + 10 [declared fail by 10 marks]
To pass the required marks => 110 + 10 = 120 marks
120 = 30 % of the total marks

The total marks required for the examination is 400.
Percentage error question and tricks
Question) Hulk multiplied a number by 3/5 instead of 5/3. What is the percentage error in the calculation?
Solution:
The formula to evaluate the error in the calculation is as shown below.

As per the question,
Correct value is 5/3 and wrong value is 3/5.

Answer : 64% error is there in the calculation.
Question ) A vendor sells 50% of apples he had. He throws away 20% of the remainders. Next day he sells 60% of he remainder and throws away the rest. What % of his apples does the vendor throws?
Solution:
Whenever we have to assume some number. It is better to assume 100
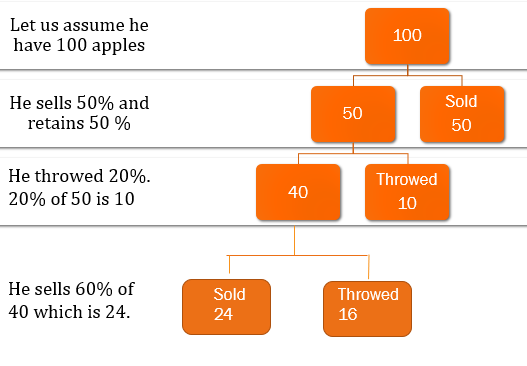
We need to find the number of % of apple does the vendor throws.
Answer: We need to add the throwed % from 3rd and 4th row.
= 10 + 16
= 26% is the apple throwed by the vendor.
All Videos playlist explaining all concepts
Practice some percentage questions now.