There is a possibility of question on the unit’s place in the question papers. The place just to the left of the decimal point in a number expressed is named as unit’s place.This article is recommended for solving the number system question of any competitive exams.
We would like to say the unit digits with the power of numbers so that a note can be made easily.
Note:
The given below is the zero to the power of anything
Zero to the power of anything will remain zero only
1. The given below is the 1 to the power of anything
The power of any number to 1 will always end in 1 only.
2. The given below are the numbers ending with the power of 2.
2 to the power of 1,5,9,13,17,21 and so on will always end with the number 2.
2 to the power of 2,6,10,14,18 and so on will always end with the number 4.
2 to the power of 3,7,11,15,19 and so on will always end with the number 8.
2 to the power of 4,8,12,16,20 and so on will always end with the number 6.
3. The given below are the unit digit of the power 3.
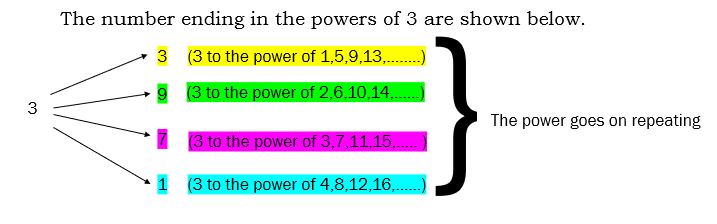
3 to the power of 1,5,9,13,17,21 and so on will always end with the number 3.
3 to the power of 2,6,10,14,18 and so on will always end with the number 9.
3 to the power of 3,7,11,15,19 and so on will always end with the number 7.
3 to the power of 4,8,12,16,20 and so on will always end with the number 1.
4. The given below are the unit digit of the power 4.
The last digit is 4 to the odd number of power. Such as 4 to the power of 1,3,5,7 and so on the last digit is always 4.
The last digit is 6 to the even number of power. Such as 4 to the power of 2,4,6,8, and so on the last digit is always 6
5. The given below are the unit digit of the power 5.
5 to the power of anything will always have 5 in the unit’s place.
6. The given below are the unit digit of the power 6.
6 to the power of anything will always have 6 in the unit’s place.
7. The given below are the unit digit of the power 7.
7 to the power of 1,5,9,13,17,21 and so on will always end with the number 7.
7 to the power of 2,6,10,14,18 and so on will always end with the number 9.
7 to the power of 3,7,11,15,19 and so on will always end with the number 3.
7 to the power of 4,8,12,16,20 and so on will always end with the number 1.
8. The given below are the unit digit of the power 8.
8 to the power of 1,5,9,13,17,21 and so on will always end with the number 8.
8 to the power of 2,6,10,14,18 and so on will always end with the number 4.
8 to the power of 3,7,11,15,19 and so on will always end with the number 2.
8 to the power of 4,8,12,16,20 and so on will always end with the number 6.
9. The given below are the unit digit of the power 9.
The last digit is 9 to the odd number of power. Such as 9 to the power of 1,3,5,7 and so on the last digit is always 9
The last digit is 1 to the even number of power. Such as 9 to the power of 2,4,6,8, and so on the last digit is always 1
Let’s dive into problems.
Question 1 ) What is the last digit of the expression
![\[ 777^7^7^7\]](https://padhle.com/wp-content/ql-cache/quicklatex.com-2b31b671ace50fc142313e8e1e99adae_l3.png "Rendered by QuickLaTeX.com")
A. 3 B. 1 C. 7 D. 9
Solution: When it comes to power always see the last two digits of the power. Here, the last two digits of the power are 77. So, as per the table, 7 to the power of 77 must end with a number of 3.
Answer: A. 3
Question 2 ) The unit’s digit of the product
![\[ 3^1^0^0^1 * 7^2^2^0^0^2 * 13^3^3^3^0^0^3 \]](https://padhle.com/wp-content/ql-cache/quicklatex.com-aa3f92d473c79499f0cc9fc7997f80c6_l3.png "Rendered by QuickLaTeX.com")
A. 3 B. 1 C. 5 D. 9
Solution: When it comes to the power as mentioned earlier we are supposed to see the last two digits of the power. If there are two-digits in the base like in the above problem 13. We are supposed to take the last digit in the base. Let’s solve it.
![\[ = 3^0^1 * 7^0^2 * 13^0^3\]](https://padhle.com/wp-content/ql-cache/quicklatex.com-11d5c5f059f68ebc07cafdbc1b4640b1_l3.png "Rendered by QuickLaTeX.com")
3 to the power of 1 is 3.
7 to the power of 2 is 49.
3 to the power of 3 is 27.
Now, let’s take unit digit in all the numbers which are 3,9 and 7.
![\[ = 3*9*7 = 189\]](https://padhle.com/wp-content/ql-cache/quicklatex.com-f0e6ab489749bf8f7449085c019eb73c_l3.png "Rendered by QuickLaTeX.com")
Find what is there in the unit’s place it is 9.
So, 9 is the answer
Answer: D. 9
Important note: 1! + 2! + 3! + 4! + 5! + 6! + 7! ………………… n!
After 5! every factorial number will end with a number 0. i.e. The unit digit will be zero after 5!
Question 3) N = 1! + 2! + 3! + 4! + 5! + …….. + 2010!. What is the digit in the unit’s place of N?
A. 3 B. 2 C. 1 D. 0
Solution: We already know that the unit digit is zero after 5!.
1! = 1
2! = 2*1 = 2
3! = 1*2*3 = 6
4! = 1*2*3*4 = 24
After 4! every factorial has zero in the unit’s place.
We have 1, 2, 6, and 4 in the unit’s place of the factorial.
= 1+2+6+4 = 13
3 is present in the unit’s place.
Answer: A. 3
Important note: Starting from 2! every factorial will end in an even digit in the unit’s place.
Question 4) The unit’s place of the product
![\[34^1^2^3! * 3456^1^2^3^4^5^6!\]](https://padhle.com/wp-content/ql-cache/quicklatex.com-90389019a5df8249302ff452add73492_l3.png "Rendered by QuickLaTeX.com")
A. 4 B. 8 C. 1 D. 6
Solution: As per the note starting from 2! every factorial will end in an even digit in the unit’s place.
So, it’s gonna be:
![\[4^e^v^e^n * 6^e^v^e^n\]](https://padhle.com/wp-content/ql-cache/quicklatex.com-8d1ef22e8cf05c8b964337787f579261_l3.png "Rendered by QuickLaTeX.com")
We know that 4 to the even power is 6 and 6 to the power of anything is 6 only.
So, 6*6 = 36.
6 is present in the unit’s place.
Answer: D.6
Now practice some number system questions now. Learn some divisibility rule of number system