Divisibility Rules – Tricks to crack Number systems questions

Number systems are the base for the maximum mathematics sums. The Number systems will act as a small step in the maximum mathematics problems. Here, we will show you the tricks which will make you go wow and fell in love with the mathematics subjects.Using these tricks crack any competitive exam.

Table of content
1) Divisibility rule by 1
2) Divisibility rule by 2
3) Divisibility rule by 3
4) Divisibility rule by 4
5) Divisibility rule by 5
6) Divisibility rule by 6
7) Divisibility rule by 7
8) Divisibility rule by 8
9) Divisibility rule by 9
10) Divisibility rule by 10
11) Divisibility rule by 11
12) Divisibility rule by 12
13) Number system questions

We need to know which number is divisible with which number to conclude to any answer.
Now, let’s roll to some divisibility tool facts.

All the natural number is divisible by 1

Is 2343 divisible by 1?
Yes, it is divisible by 1.
All the natural numbers are divisible by 1.

Divisibility tool of 2 = It has to be an even number.

Let’s see if 24 is divisible by 2.
Yes, it is divisible by 2.
Same wise, All the even numbers are divisible by 2

Divisibility tool of 3 = Sum of digit should be a multiple of 3.

Let’s see if 345 is a multiple of 3:
Our trick says to add the number and see if it is a multiple of 3.
Now, 345 = 3+4+5 = 12 which is a multiple of 3.
If you still don’t know if 12 is a multiple of 3. Let’s add again.
Now, 12 = 1+2 = 3 which is a multiple of 3.

Divisibility tool of 4 = Last two digit should a multiple of 4.

Our trick says that last two-digit should be a multiple of 4.
Let’s see if 546466524 is divisible by 4?
Yes, it will be divisible of 4. The last two numbers are 24 which is a multiple of 4.
Please comment on the answer in the comment box.

Divisibility tool of 5 = Last digit to be either 0 or 5.

Our trick says that the last digit has to be 0 or 5.
Let’s see if 54473556805 is divisible by 5?
Yes, it will e divisible of 5. The last digit is 5 so, it will be divisible by 5.
Please comment on the answer in the comment box.

Let’s see if 54545410 is divisible by 5?
Yes, it will be divisible of 5. The last digit is 0 so, it will be divisible by 5.
Please comment on the answer in the comment box.

Divisibility tool of 6 = The number have to be even and the digits to divisible of 3 & 2.

Our trick says that the numbers have to be even and the digits to be divisible of 3 & 2.
Let’s see if 324.
The first condition says that the number has to be even. Is 324 an even number? Yes, it is an even number.
The second condition if it is divisible by 3? Yes, it is a multiple of 3 and the answer is 108.
The third condition if it is divisible by 2? Yes, it is a multiple of 2 and the answer is 162.
So, 324 will be divisible by 6.
Comment the answer in the comment section.

Divisibility tool of 7 = As shown below.

Let’s see if 343 is a multiple of 3:

The first step is to take the one’s digit place and multiple it by 2 and subtract it with the remaining number.
So in 343, 3 in digit place will be multiplied by 2 and be subtracted from the remaining left number which is 34 as shown below.
34 – 3×2 => 34 – 6 = 28
We know 28 is multiple of 4.
So, we can conclude that 343 is divisible by 7.

Divisibility tool of 8 = Last digit has to be even and last three digit has to be a multiple of 8.

Our trick says that the last digit has to be even and the last three-digit has to be a multiple of 8.
Let’s see if 435296 is a multiple of 8?
The first condition says that the last digit has to be even and in the above example 296, 6 is an even number.
The second condition says that the last three-digit has to be a multiple of 8. If 8 multiplied with 37 then the value is 296. So, the above example satisfies all the condition.
So, 435296 is divisible by 8.

Divisibility tool of 9 = Sum of digits has to be a multiple of 9.

Our trick says that the sum of all numbers has to be a multiple of 9.
Let’s see 4545667 is divisible by 9?
Let’s add all the numbers: 4+5+4+5+6+6+7 = 37.
And we know 37 is not a multiple of 9. So, 4545667 is not divisible by 9.

Let’s see if 566750988 is divisible by 9?
Let’s add all the numbers: 5+6+6+7+5+0+9+8+8 = 54.
And we know 54 is a multiple of 9. So, 566750988 is divisible by 9.
Comment the answer in the comment section.

Divisibility tool of 10 = The last number has to be 0.

This is a simple trick that everyone knows. If a number ends with 0 it will be divisible by 10.
For example, 556446990 is divisible by 10.

Divisibility tool of 11 = The difference between the sum of the alternate number has to be 0 or 11.

The difference between the sum of the alternate number has to be 0 or 11.
Let’s see if 12496 is divisible by 11?

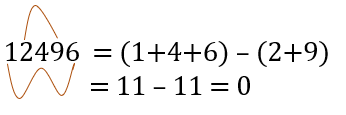
rule of divisibility by 11 - number system hack

Hence, we can conclude that 12496 is divisible by 11.

Divisibility tool of 12

12. Divisibility tool of 12 = The number has to be a multiple of 4 & 3.
The number has to be a multiple of 4 & 3.
Let’s see if 988 is divisible by 12?
The first condition says that the number has to be a multiple of 4. Is 988 divisible by 4? Yes, 988 is divisible by 4 and the dividend is 247.
The second condition says that the number has to be a multiple of 3. Is 988 divisible by 3?
No, 988 is not divisible by 3 and that dividend is 329.33. It comes in decimal.
So, 988 is not divisible by 12.

Let’s see if 9888 is divisible by 12?
The first condition says that the number has to be a multiple of 4. Is 9888 divisible by 4? Yes, 9888 is divisible by 4 and the dividend is 2472.
The second condition says that the number has to be a multiple of 3. Is 9888 divisible by 3? Yes, 9888 is divisible by 3 and the dividend is 3296.

We can conclude that 9888 is divisible by 12.

If all above mentioned rules are clear then let’s roll into some number system questions.

Number System Questions

Question 1 ) Which one of the following numbers is divisible by 8 & 11.
A) 12496 B) 414206 C) 999000 D) 38400

Solution: In these type of questions we can go only by the options.
Use divisibility rule of 8
A.

$12496 = \frac{496}{8} = 62$

So, 12496 is divisible by 8.

Now let’s see for 11 – Use divisibility rule of 11

$12496 = (1+4+6) - (2+9) = 11 - 11 = 0$

So, 12496 is divisible by 11.

So, 12496 is divisible by both 8 & 11

Answer: A

Question 2 ) Which of the following numbers is divisible by each one of 3, 7, 9 & 11?
A. 639 B. 2039 C. 37911 D. 7911

Solution: As mentioned earlier we got to go via options.
A. 639
If it is divisible by 3

$639 = 6+3+9 = 24$

And 24 is divisible by 3.
So, 639 is divisible by 3
If it divisible by 7

$639 = 63 - 9*2 = 63 - 18 = 43$

639 is not divisible by 7. So, the answer can’t be A

B. 2079
Let’s see if it is divisible by 3.

$2079 = 2+0+7+9 = 18$

So, 18 is divisible by 3.
So, 2079 is divisible by 3.

Let’s see if 2079 is divisible by 7.

$2079 = 207 - (9*2) = 207 - 18 = 189$

$189 = 18 - (9*2) = 18 - 18 = 0$

So, 189 is divisible by 7.
So, 2079 is divisible by 7.

Let’s see if 2079 is divisible by 9.

$2079 = 2+0+7+9 = 18$

So, 18 is divisible by 9.
So, 2079 is divisible by 9

Let’s see if 2079 divisible by 11.

$2079 = (2 + 7) - (0 + 9) = 0$

So, 2079 is divisible by 11.

So, 2079 is divisible by 3, 7, 9 and 11.

Answer: B

Question 3 ) What is the value of M and N respectively if M39048458N is divisible by 8 & 11? M and N being single-digit integers.
A. 7,8 B. 8,6 C. 6,4 D. 5,4

Solution: In this question, it is better to find M and N by11 first. Use here the divisibility rule of 11.

Options B and C are divisible by 11.
Now, lets if those options are divisible by 8.
Let’s see if option B works for 8.
M394048458N
B. 8, 6
Let’s put 8 as M and 6 as N.
M394048458N
83940484586; Now in order to get it divided by 8 we know that our trick is to find if the last three digits are divisible by 8.
Now, let’s see 586 is divisible by 8.
586 is not an exact divisible by 8. The answer arrives in decimals.
So, answer B is not the correct answer.

Now, only option C is left. It must be the correct answer.
Let’s see if we can get it right.
Substitute option C 6 and 4 in M and N respectively.
So, now the equation becomes
639404848584
Now, let’s see 584 is an exact divisible by 8 and the dividend is 73.
Option C is the correct answer.

Answer: C

Question 4 )

$10^25 - 7 is divisible by _______$

A. 3 B. 9 C. 2 D. A&B

Solution: It is a bit common sense question
Now, we know that 10 to the power of anything will end by up in 0.
As per the question, there will be en-numerous zero.
Now, if it is subtracted by 7. The last two digits will be 93.
In the given options only 3 can divide 93 exactly without decimal.
So, the only option correct is A.

Answer: A.

Question 5) How many factors does 48 have, excluding 1 and 48?
A. 12 B. 4 C. 8 D. 10

Solution: In order to do the factors we need to do LCM. Let’s see how the LCM looks.

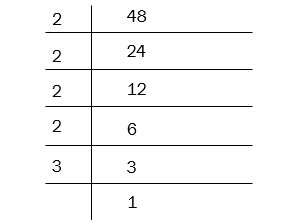
Now you could see 2 is repeated 4 times and 3 is repeated 1 time.
So, here is the answer

$2^4 * 3^1$

In order to find the factor add the power with 1 and multiply with it as shown below.
What is the power of 2? It is 4
What is the power of 3? It is 1

Now, add one to both the powers and multiply.
So, the answer would be
(4 + 1) * (1+1) = 5 * 2 =10

There are 10 factors for 48. If you mark 10 in the option then you are wrong.
As the question mentioned we need to exclude 1 and 48.
The correct answer = 10 – 2 = 8.

Answer: C

number-systemLearn some tricks how to find unit’s place digit of a number

Join Telegram for Updates