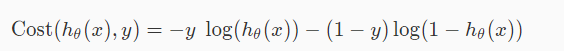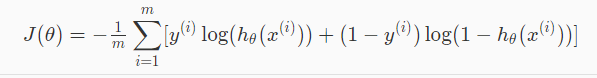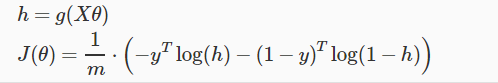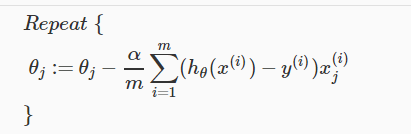So in the last post we have seen about what are the classification problems, hypothesis function and cost function in classification problems.
Now in this post we we will see about simplification of that cost function and how to apply gradient descent to fit the parameters of logistic regression.
Simplified Cost Function
In the last post we have written the cost function in two lines.one case for y=1 and another case for y=0.But we can write combined equation which will work out for both condition’s y=1 and y=0 as following:
If we have y=0 then the first term will cancel out and we were left with –log(1−hθ(x)) and if we have y=1 then the second term will cancel out and we were left with −log(hθ(x)) which is exactly same as we learn in earlier post.
So by putting the above term in our cost function we can write full cost function as following:
A vectorized implementation of cost function will look as following:
Gradient Descent
Now we have our cost function,we will apply a gradient descent to get minimum cost function. We will get the gradient descent for the above cost function as following, which is identical to the one which we used in linear regression but we have different hypothesis function than we have in linear regression.
Advanced Optimization
We will check some advanced optimization which can be used to run logistic regression faster than it’s running using gradient descent.
You can check some other optimized algorithm like BFGS, L-BFGS which are better in some situation than gradient descent.
Multi class Classification
In this we will see how to get a logistic regression that will also work in case of multi class classification problems. We will discuss one algorithm called One-vs-all classification.
Here are some example to multiclass classfication problems.
- Suppose we want to classify emails into different folder like work email’s,family email’s,friend email’s.So we have a classification problem with four classes.
- We want describe whether as a sunny, cloudy, rain,snow.Again with four classes.
So one-vs-all classification can be summarized as following:
We have to train our logistic regression classifier hθ(x) for each class to predict the probability that is y = i .After training a classifier we can make a prediction on a new x and can pick the class that maximizes hθ(x).
The Problem Of Overfitting
The logistic regression and linear regression will work well for many problems,but for certain machine learning problems they ran into a problem called over fitting that can cause them to perform them very poorly.
When the form of our hypothesis function h maps poorly to the trend of the data,we call it under fitting or high bias.This underfitting will be caused by the function’s that used too few features only.And When the form of our hypothesis function h fits to the trend of the data,we call it over fitting or high bias.This overfitting will be caused by the function’s that used too many features only.
We can have two solutions to address this problem of overfitting:
- We can reduce the number of features in our model by manually selecting which features and to keep.
- We can apply the regularization by keeping all the features but reducing the magnitude of parameters θj.
This is all about simplified cost function and multi class classification problems.