Allegation method makes us to find out the final ratio of two or more ingredients to derive at a particular mixture at a desired price.
The following is the trick or the method in which we will be solving the questions.
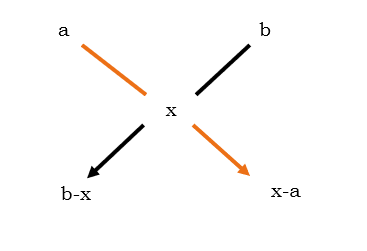
Note – A and B is a quantity. A > B and X is the value always lie between A and B. B – X and X – A is ratio.
The above pic will be more understandable when we solve some questions.
Allegation and Mixture questions
Question 1 ) In what ratio must a grocer mix two varieties of pulses costing Rs. 15 and Rs. 20 kg respectively so as to get a mixture worth 16.5 kg?
Solution: As per the consideration to the above pic 15 is considered to be ‘a’, 20 to be considered as ‘b’, and 16.5 as the mixture expected that as ‘x’.
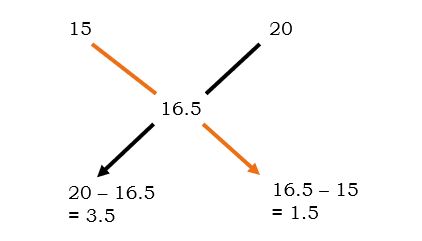
The required ratio at the desired price is in the ratio of 3.5 : 1.5. The options can either be 3.5 : 1. 5 or in the multiples of 3.5 : 1.5. So, please pay attention to the options.
Answer: 3.5 : 1.5
Question 2 ) The ratio in which 35% of alcohol solution should be mixed with 45% solution in order to get a 41% solution?
Solution: As per the question.
‘a’ = 35
‘b’ = 45
‘x’ = desired mixture = 41
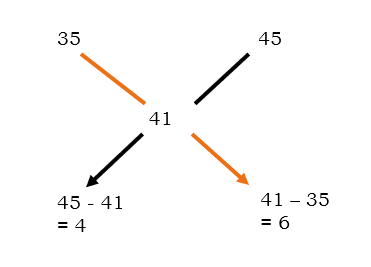
The required ratio at the desired mixture is 4 : 6.
Answer: 4 : 6
Question 3 ) A dealer buys 11 kg of wheat at Rs. 374 and mixes it with another quality of wheat in the ration of 4 : 3. The price of the resulting mixture Rs. 40 per kg. The price of the other quality of wheat is ____?
Solution: Price of 11 kg Rice is =374 , Price of 1 Kg = 374 /11 = 34 , hence ‘a’ = 34
X = resulting mixture price = 40
B = ?:
Ration of a : b = 4 : 3 = assume these values as 4x and 3x .
now from below diagram = 40 – 34 = 6 = 3x , x = 2
4x = 4 * 2 = 8
40 + 8 = 48 is the answer
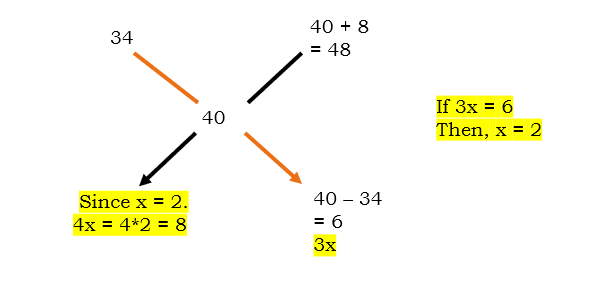
Since the desired ratio is given as 4 : 3. So, we have mentioned it as 4x and 3x.
We found the ‘a’ by unitary method and then cracked the x.
Then we found out ‘b’ by substituting x.
Answer: 48
Question 4 ) A milk vendor has 2 cans of milk. The first contains 25% of water and the rest milk. The second contains 50% water. How much milk should he mix from each container so as to get 12 litres of milk such that the ratio of water to milk is 3 : 5?
Note – Two quantities are in ration A:B and total quantity is C ,
then total share of A is A/(A+B) * C
then total share of B is B/(A+B) * C
Solution: In the first can there is 25% of water and in second can there is 50% of water. Total solution is 100 %.
In the first can there is 75% of milk and in second can there is 50% of milk.
Lets solve this question with Water only
Water to milk ratio in mixture = 3 :5 , Total solution = 100 %
Total water in mixture = 3 / (3 + 5) * 100 = 3 /8 * 100 = 37.5
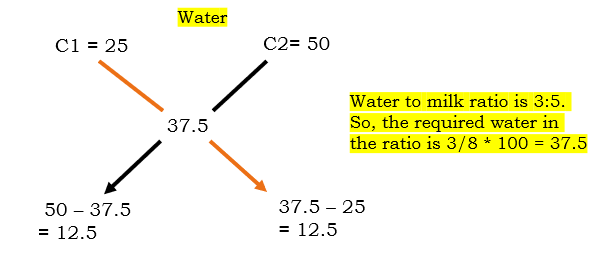
The required ratio is 12.5 : 12.5 = 1 : 1
Answer: 1 : 1
Even if we solve via milk we will get the same ratio as the ratio of water.
Total milk share in mixture = 5 / ( 3 + 5 ) * 100 = 5 /8 * 100 = 62.5 as explained above.
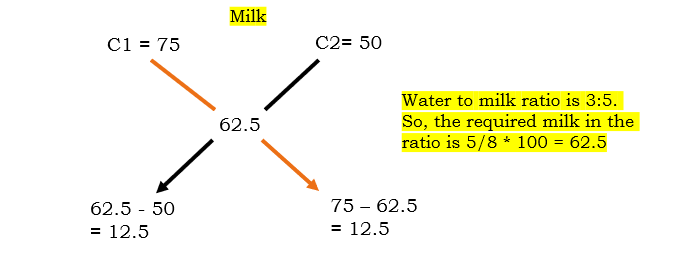
Even here the ratio is 12.5 : 12.5 = 1 : 1.
In exams you don’t have to solve both for milk and water. Solve any one and get the answer.
Answer: 1 : 1
Question 5 ) A shopkeeper has 50 kg of rice. He sells a part it at 20% of profit and the rest at 40% of profit. He gains 25% on the whole. Find the ratio of the two parts.
Solution: When no value is mentioned , take value as 100 to ease the calculation.
Considering if his selling price was 100. Then the 20% of profit would be 120, 40% of profit would be 140 and 25% on the whole would be 125.
‘a’ = 120
‘b’ = 140
‘x’ = 125 (Desired mixture)
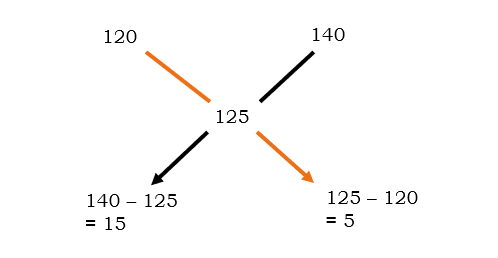
The desired mixture is 15 : 1. If we reduce we will get the answer as 3 : 1.
Answer: 3 : 1
Mixture and allegation question 3 quantities types questions
Question 6 ) In what ratio must a grocer mix three varieties of sugar costing Rs. 50, Rs. 70 and Rs. 80 per kg respectively so as to get a mixture worth Rs. 60 per kg?
Solution : When we have 3 quantities in a mixture and we need to find a ratio –
The resultant mixture should be Rs 60 per kg , now just divide all the given mixture wrt to 60 now .
mixture lesser than 60 = 50
mixture greater than 60 = 70, 80
Resultant mixture is 60 .
Now make the sets like – { mixture lesser than resultant } * { mixture greater than resultant }
Here – { 50} * { 70,80 } =>
Now divide like this => { 50 ,70 } and { 50 , 80 }
so we have two sets now and solve like below
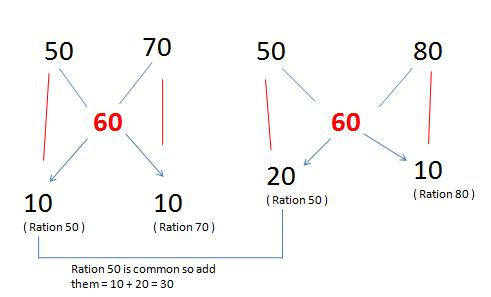
Ratio 50 : Ration 70 = 10 : 10
Ratio 50 : Ration 80 = 20 : 10
Now simply add ration of the common one that is Ration 50 as shown in above image
Ration 50 = [ 10 + 20 ] = 30
Ration 50 : Ration 70 : Ration 80 = 30 : 10 : 10
The required ratio at the desired mixture is 30 : 10 : 10. If we reduce it, the answer will be 3 : 1 : 1.
Answer: 3 : 1 : 1
Solve some mixture and allegation questions now.